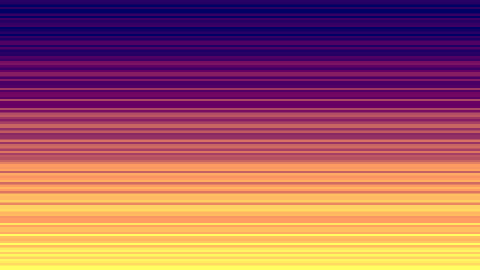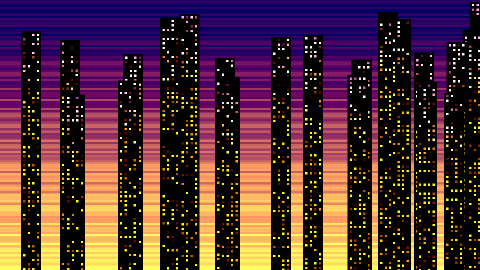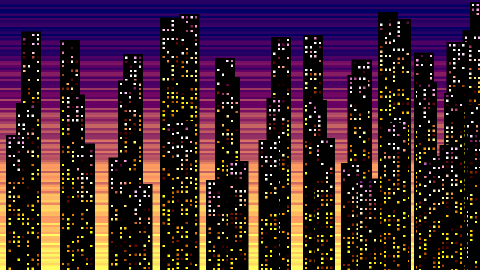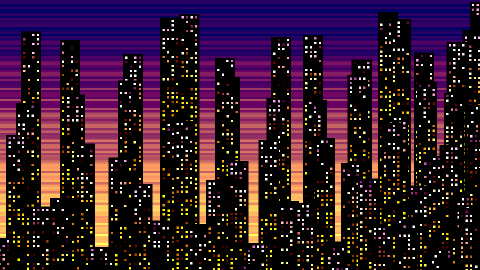
Hello, tiny coders, I’m back with another dwitter dissection! Today we will explore the JavaScript code that produces this beautiful procedurally generated cityscape.
for(z=k=2e3;k--;x.fillRect(i*9+S(z*t)*z|0,j*9+t*420,t?9:z,9))i=k%9,j=k/9|0,x.fillStyle=R(q=t?i*j%2*400*S(k*k*t):k/3+C(k*k)*39,q-99,t?q-k:99)
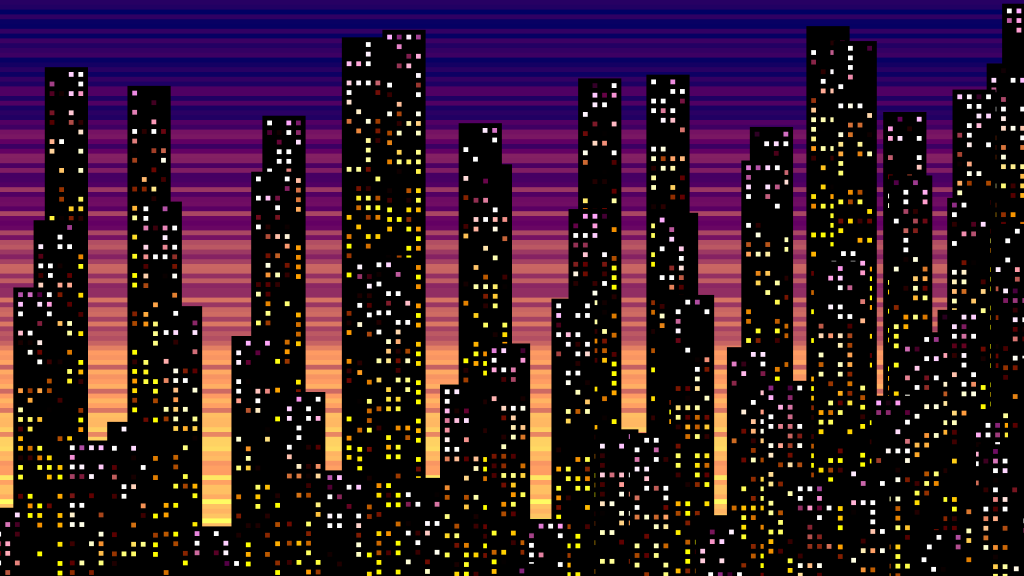
Continue reading on for a full explanation of how it was made!
Cityscapes are a type of landscape that represent an urban area. They tend to lend themselves well to procedurally generation and have inspired many amazing works of art. Here is the actual dweet running live in an iframe. You can play around with the code while we examine how it works.
Before we get into the details, lets reformat the code so it’s easier to read. Here’s a link to open this cleaner code in my personal JavaScript editor CapJS.
for( z = k = 2e3; k--; ) // loop
i = k % 9, // grid X
j = k / 9 | 0, // grid y
x.fillStyle = R( // set color
q = t ? i*j%2*400*S(k*k*t) : k/3+C(k*k)*39, // red
q-99, // green
t ? q-k : 99), // blue
x.fillRect( // draw rect
i*9 + S(z*t)*z | 0, // pos X
j*9 + t*420, // pos Y
t ? 9 : z, 9 ) // size
At a high level the code has two modes of operation. On the first frame it draws the background sunset. Then on subsequent frames it renders a building with randomly colored windows, moving farther down the canvas each frame until the image is finished. It does both of these things with code that is shuffled together to save space, let’s see how that works.
for( z = k = 2e3; k--; ) // loop
The for loop iterates over k from 2e3 (2000) to 0, and also sets z to 2000 to be used later. The value 2e3 was chosen to be larger then the canvas width which is 1920 pixels.
i = k % 9, // grid X j = k / 9 | 0, // grid y
Each building is 9 squares wide, so we can convert k to i and j representing the X/Y position in a 2D grid. The |0 operation is necessary to convert j to an integer. A simpler option is to use separate loops for i and j, but doing it like this is a common technique that saves a few bytes.
x.fillStyle = R( // set color q = t ? i*j%2*400*S(k*k*t) : k/3+C(k*k)*39, // red q-99, // green t ? q-k : 99), // blue
There are two different coloring modes. On the first frame the background is drawn to represent a sunset by checking if time (t) is 0. For subsequent frames the building’s coloration mode will be used. The R function provided by Dwitter is equivalent to the template string `rgba(${r},${g},${b})`. Each color channel takes a value between 0 and 255, higher or lower values are clamped.
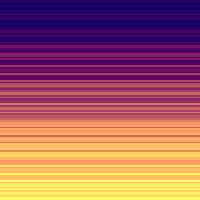

Let’s talk about the background render that happens on frame 0 first. The red channel creates a gradient using k/3 so the red increases towards the bottom. A bit of randomness is added using the cosine function C(k*k)*39. The amazing chaotic nature of trig functions when passed a powered integer is a great way to get pseudo random values and much smaller then using Math.random().
To get an orangish sunset color it needs some green but less then red, so we just subtract 99 from the red. This results in a black towards the top, blending to dark red, orange and eventually yellow at the bottom.
The blue channel is simply set to a constant value of 99. The number 99 is used often in dweets because it is the largest 2 digit number possible. Combining all three color components allows a dark blue to shine through at the top blending to a bright yellow at the bottom, hopefully evocative of a cloudy sunset.


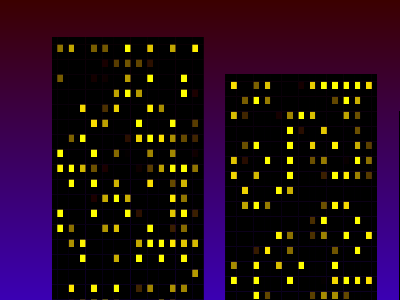
Every frame after the first a single randomly positioned building is drawn using a 2D grid of squares. To create the lit windows with black outlines, we need every even numbered rows and columns (j or i) to be black which is done using the code i*j%2 also equivalent to (i*j)%2 which returns 0 if either i or j is even. To add randomness we use the trig sine function 400*S(k*k*t) but also incorporating t so each building will have a different colored windows. Another effect of using sine is that half of the values will be below 0, causing those windows to be black.
The green component for windows is the same as the background, always 99 less then the red which gives a red-yellow-white gradient. A touch of blue is applied by subtracting k from the red value, allowing some purple tones to sneak through towards the top when k approaches 0.
x.fillRect( // draw rect i*9 + S(z*t)*z | 0, // pos X j*9 + t*420, // pos Y t ? 9 : z, 9 ) // size
Here is where the scene is actually drawn. Again, this code works a bit different for the first frame in order to create the background sky gradient. The only functional difference is that instead of squares, it renders horizontal lines using the width value of z which is set to 2e3, enough to stretch horizontally across the canvas. The side effect of time (t) being 0 is the code simplifies to x.fillRect(i*9, j*9, z, 9), which allows the background to cover the entire canvas as j ranges from 2000/9 (222) to 0.
On subsequent frames it will use the building’s color mode and draw a 9 x 9 squares to create the windows and black frame surrounding them. Each building’s X position is offset by the code S(z*t)*z which generates a pseudo random value between -2000 and 2000. Also each building is drawn slightly farther down the canvas by adding the value t*420 to the Y component, or 7 pixels per frame at dwitter’s 60 fps. The buildings are sometimes drawn on top of each other which helps to create interesting variety and disguise that fact that each building is the same exact width.
That’s all there is to it! Feel free to play around with the code and experiment, in my experience that’s the best way to learn. You may also be interested to know that I didn’t just whip up this dweet from nothing, but went through several drafts. Here’s the first one I posted, you can probably see how it evolved.
Let’s take one last look at the minified code, hopefully it makes slightly more sense now…
for(z=k=2e3;k--;x.fillRect(i*9+S(z*t)*z|0,j*9+t*420,t?9:z,9))i=k%9,j=k/9|0,x.fillStyle=R(q=t?i*j%2*400*S(k*k*t):k/3+C(k*k)*39,q-99,t?q-k:99)
I will leave you with a more recent dweet that flys through this incredible 3D city scene. Until next time, remember there are no small programs, only small programmers. Keep on dweeting!








Pingback: Dissecting a Dweet #9: City Sunset – Tiny JavaScript Analysis - GistTree
Pingback: Dissecting a Dweet #9: City Sunset – Tiny JavaScript Analysis – Full-Stack Feed
Pingback: Collective #630 – Find Right Software
Pingback: Web Design & Development News: Collective #630 | Codrops
Pingback: Collective #630 - Coduza - Blog
Pingback: Collective #630 - GB YouTube - Blog
Pingback: Collective #630 – Enjoy Web