On the popular YouTube math channel StandUpMaths, they recently asked: How thick would a coin need to be so it landed on it’s side 1/3 of the time, making it a fair three sided coin?
It turns out, this is difficult to predict mathematically and they weren’t able to come up with a decisive answer. So I wanted to try simulating the experiment, to do thousands of flips and track the results. Keep reading for the full explanation and a reasonable stab at the answer.
StandUpMath’s Video
I recommend watching the original video, but in the end they came up with 2 totally different solutions using math: 2 root 2 and root 3. In decimal that comes out to D * 0.35 and D * 0.577, largely different results. They flipped both of those coins 1000 times each and didn’t get definitive results. So they went on to create a campaign to crowd source coin flips to gather more results and home in on the answer.
Setting Up the Experiment in UE4
Flipping a massive number of coins in real life is a laborious task. To get anything close to an accurate answer, we need to flip hundreds of coins thousands of times and track their results. This is a good problem for a computer simulation, and the setup in UE4 is very simple.
A coin object is composed of a physics cylinder, with fixed diameter and variable length. Coins do not collide with each other and use CCD for more accurate physics. Detecting which side is up is done simply by looking at the Z component of the coin’s up vector.
A coin tester object controls the experiment by flipping coins and storing results in an array of structs that track how often each coin landed on each side. Results are just printed out to the log after each iteration. I just copy/paste the results from the log to notepad and uploaded to Google sheets as a csv.
You can download my UE4 project files here. (UE 4.18 required)
Physical Simulation
There are several physical properties that I tried to take into consideration. The coin’s initial linear velocity is randomized and applied in a random cone pointed up. The angular velocity is also randomized and applied mostly along the horizontal axis of the coin, to help recreate how coins are normally flipped.
The coin is actually much larger then a real coin relative to gravity because I was having simulation anomalies when I reduced the coin size or increased the gravity by much. This could probably be improved by reducing the physics time step, but that would also slow down the simulation. I left most physical properties at their default, except for the restitution which I reduced to .2 to more accurately represent a metal coin. I ran the test at an accelerated global time scale, to speed it along.
Results Analysis
I set up the simulation for coins of length D*.01 to D * 1.0, in .01 increments, 100 coins representing all the lengths up to D. I let it run for 9000 iterations, it took about 10 hours.
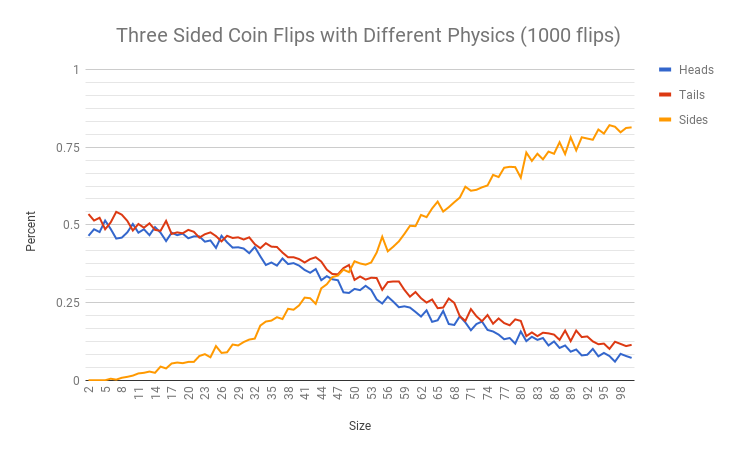
I graphed all the results in a Google spreadsheet.

This data suggests an optimum side length of around D * .54. Interestingly the percent chance of landing on it’s side seems to be linearly related to the length of the side, though clearly it would need to eventually taper off. The graph also shows the expected result that very thin coins never land on their side with heads and tails being roughly equal.
The slightly higher probability of tails for thinner coins seems unexpected, but it is probably caused by the coins always starting tails up. I have heard that coins are slightly more likely to land on the side they started on, so it’s cool to see that here. I’m not sure why it seems to be slightly the opposite for thicker coins though.
To verify the results I set up a second experiment. This time with many parameters changed: less gravity, much more angular velocity on all axes, higher restitution, higher start position, etc. The results were similar but skewed slightly lower, suggesting a size of around .48. My guess is that the biggest difference was greatly increasing the angular velocity, especially along the vertical axis which would cause coins to roll more. Also, interestingly the graph seems less linear with the tapering being more obvious. Tails is also consistently appearing more often then heads as in the first set of results.
Conclusion
I can’t say how accurate this simulation is compared to reality, though it is probably at least slightly off. These are perfect coins with no air resistance or other factors to consider Also the random values were chosen to flip the coin are just guesses about how a coin would be flipped. However with two very different physics settings both sets of results mostly agree on a value between .47 and .54.
More experiments need to be done to compare different physics parameters. Also interesting would be seeing results from a 2 sided coin, if the starting side up is more likely to be landed on. Additionally it would be helpful for someone else to verify my results, it’s very possible that I’ve just made a mistake somewhere. My UE4 project is available for anyone interested.
After doing this experiment, I have to conclude that a fair three sided coin is simply not possible outside of an extremely controlled environment. Even a two sided coin is shown by the data to be slightly biased. In a realistic scenario there too are many uncontrollable physical factors that can cause a coin to be more or less likely to land on its side, including what actually constitutes a flip. But if you wanted to ball park it, this might be a good place to start.






The bias you found is consistent with Diaconis’s research:
https://www.youtube.com/watch?v=AYnJv68T3MM