How I made a 1K Pinball Game in JavaScript – Lu1ky Pinball

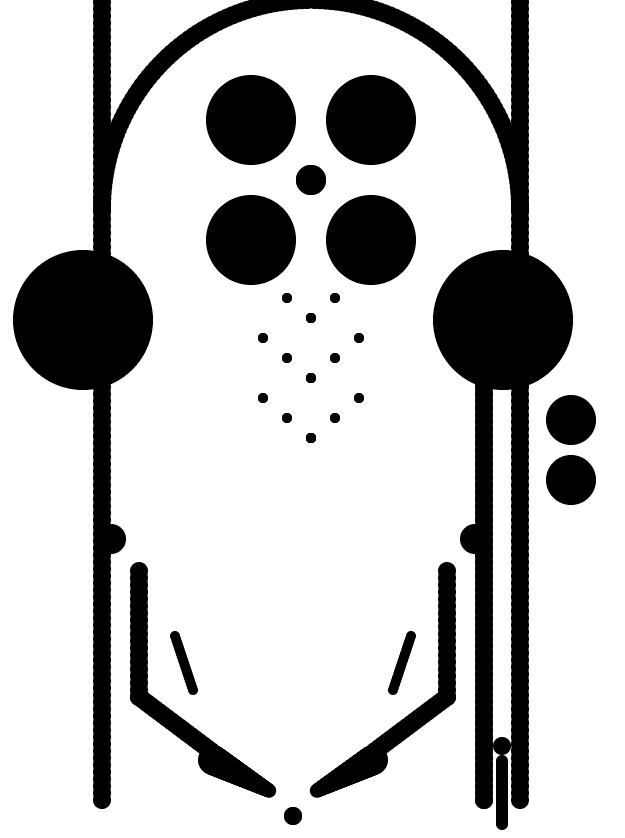
I’ve made quite a few 1k games now, yet I always find room for improvement and there is so much more to explore in this space. For the JS1024 contest this year the theme was Lucky and I made a tiny pinball machine. It received 1st place in the JavaScript category! I have been wondering for a while how realistic of a pinball sim could be achieved with such a limited amount of code.

This post will walk you through every line for my tiny pinball game that fits in 1 kilobyte of JavaScript. How much is 1k you ask? This much…

for(_='00F*rE8F-7ED/f)*hCin(BMath.AAsB@keyZ1,Y0,XXYWr=V),UUVT-rS69R15Qe. a.f- r-r-=()**Acos(x,y,t, w x ge=n[--;)for();209+=+rw(482(2*h-1)EU+*(1,X9))60	n[h] y=a=>n[Z]=h=2;h*,;rU5Fc.beginPath(c.fill(c.arc(
w=(V9)=>n.push({r,g:Xw:0}n=[x=3,1],i=g=X1e3T65{);RY79XX6)}{,816,18WQ+	12W45+	24W45U-21032W70T1Q5F+D+182539,YQT	673,D+*r/38U-*@r/38)V19+Q4R7-754-4EUR7+3FUR0-3E,Y5%3*24438S%9*2W5)}onZdownYonZupXsetInterval(`w=9;w{=Amax(-YAmBYn["zx"[h]]?-.07:.05)T653+65*h],=-+(=482+*(80S/2))U=-+(=7	*@/2)U VQS/8,133],=AmB790,=n.c?.05:@++i)/99+(7	-)/19);width|=2],,.F17,1e3<&&x&&(=RY=74X==Xx--Un.map((a=>{w||
x,y,b?--b+r:rUf=Ahypot(y=-x,o=-yTg-,t=w-,0>&0<r*y+t*o&!(t&!)&&(y/f,o/f,f*=f/(t*yS*oUh=!t|b?1.3:(b=9,	0<y||(++g%64||++xU1.7U(r+oC,(t-yC)}))}Vg+8>>3
2	S%8*2X420+3E,r?9:g%8Vx
7	,420+	E,25)`,16)';G=/[
- Q-Z@-F]/.exec(_);)with(_.split(G))_=join(shift());eval(_)

That’s how the code looks after being fully minified, though no one would be expected to recognize it at that point. In addition to being minified, it has also been regpacked which is a special tool for size coding that can create compressed JavaScript code that can uncompress itself.

What does it all mean? Keep reading to find out.

Let’s take a look at the original code before it has been minified. We will go through the entire JavaScript file line by line. This code is also available on GitHub.

'use strict';

// js1024 shim
const a = document.createElement('canvas');
const c = a.getContext('2d');
document.body.appendChild(a);
a.width = innerWidth;
a.height = innerHeight;

This first part is not included in the 1024k build. It is automatically created by the JS1024 shim which uses the same rules as the JS1k competition. This is where it creates the canvas and sets it to the canvas size to fill the window.

I always use strict mode for my JS code, but that will also be removed in the final build, allowing for even more space savings.

// constants (will be auto replace in minified)
const TABLE_WIDTH = 800;
const TABLE_HEIGHT = 800;
const MAX_BALL_HEIGHT = TABLE_HEIGHT+200;
const CENTER = TABLE_WIDTH/2+100;
const BALL_RADIUS = 9;
const WALL_RADIUS = 9;
const DOME_RADIUS = 200;
const FLIPPER_RADIUS = 15;
const FLIPPER_PIECES = 65
const FLIPPER_SPACE = 80;
const FLIPPER_CENTER = CENTER-BALL_RADIUS-WALL_RADIUS;
const FLIPPER_HEIGHT = TABLE_HEIGHT-40;
const SHOOTER_HEIGHT = TABLE_HEIGHT-40;
const SHOOTER_MAX_HEIGHT = TABLE_HEIGHT-10;
const FLIPPER_COUNT = 2;
const BALL_INDEX = FLIPPER_COUNT;
const RESTITUTION = 1.3;
const BUMPER_RESTITUTION = 1.7;
const PHYSICS_SUBSTEPS = 9;

// object types
const TYPE_WALL       = 0;
const TYPE_BUMPER     = 1;

These are all the constants for the game. None of this will appear after the code has been minified because all these values will just be used in place. It makes it easier for me to tweak things when all the constants are at the top.

// locals (remove from minified)
let i, j, dx, dy, s, h, o, frame;

// global variables
let objects, score, ballCount;

This is where all of the variables used by the game are declared. There are no internal variables used in any of the functions. This way all these declarations can be removed from the final build. As an added bonus the keywords to declare objects like let, var, and const will also not be needed.

// spawn object
let makeObject =
(
    x, y,          // position
    t,             // type
    r=WALL_RADIUS  // radius
)=> objects.push({x, y, t, r, v:0, w:0});

There are only two functions used by the game. The makeObject function is how we create the level and everything in it. It just creates and object and puts it in a list. The object has 6 parameters…

• x & y stores the position
• t is the type of object which is just 0 or 1
• r is the radius of the object for both drawing and collision
• v & w are the x and y velocity respectively, set to 0 on creation

let drawCircle = (x,y,r)=> c.beginPath(c.fill(c.arc(x,y,r,0,9)));

Everything in the game is drawn as a circle. In the build, this function will be inlined to remove the declaration. So in the final build “c.beginPath(c.fill(c.arc(” will appear three times.

Even though it seems to take more space, after compression it ends up saving space because the exact copies of the code compress very well. This is a good thing to keep in mind when writing size code that will compressed.

// int global variables
objects = [ballCount = 3, 1];

// make ball and init
makeObject(frame = score = 0, MAX_BALL_HEIGHT);

This is where we create the list of objects, and set a few variables such as the ball count to 3 and score to 0.

We also make the ball object which is the first object in the list, and place it at the very bottom of the table so it will respawn on startup.

// flippers and shooter
for(i = FLIPPER_PIECES; i--;)
{
    for(s=FLIPPER_COUNT;s--;)
        makeObject();
    makeObject(CENTER+DOME_RADIUS-BALL_RADIUS,SHOOTER_MAX_HEIGHT, TYPE_WALL, 6);
}

Next we create the flipper and shooter pieces which will be driven by code in the update loop.

// build symmetric table
for(s=2;s--;)
{
    // bottom pin
    makeObject(FLIPPER_CENTER, FLIPPER_HEIGHT+56);

    // score bumpers
    const BUMPER_CENTER = 180;
    makeObject(CENTER, BUMPER_CENTER, TYPE_BUMPER, 15);
    makeObject(CENTER+(s*2-1)*60, BUMPER_CENTER-60, TYPE_BUMPER, 45);
    makeObject(CENTER+(s*2-1)*60, BUMPER_CENTER+60, TYPE_BUMPER, 45);

    // side bummpers
    makeObject(FLIPPER_CENTER-(s*2-1)*210, DOME_RADIUS+120, TYPE_BUMPER, 70);

    // safety bumpers
    makeObject(FLIPPER_CENTER+(s*2-1)*182, FLIPPER_HEIGHT-221,TYPE_BUMPER,15);

Then we build out the pinball table in a symmetric way. By looping twice we can do the left and right side with the same code. First we set up the scoring bumpers.

    // side walls
    for(i=115;i--;)
        makeObject(CENTER+(s*2-1)*(DOME_RADIUS+WALL_RADIUS),TABLE_HEIGHT-7*i);

    for(i=60;i--;)
    {
        // shooter wall
        makeObject(CENTER+DOME_RADIUS-BALL_RADIUS*2-WALL_RADIUS,
            TABLE_HEIGHT-7*i);
            
        // top dome
        const DOME_BOTH_RADIUS = DOME_RADIUS+WALL_RADIUS;
        makeObject(
            CENTER+(s*2-1)*DOME_BOTH_RADIUS*Math.cos(i/38),
            DOME_BOTH_RADIUS-DOME_BOTH_RADIUS*Math.sin(i/38));
    }

To make walls we loop again to create a dense row of objects. Everything is still composed of circles but since they are so close together the physics will treat them like a straight line.

    for(i=19;i--;)
    {  
        // flipper lane side
        makeObject(FLIPPER_CENTER + (s*2-1)*(FLIPPER_SPACE+74),
            FLIPPER_HEIGHT-63 - i*7);

        // flipper lane bottom
        makeObject(FLIPPER_CENTER + (s*2-1)*(FLIPPER_SPACE+74-i*4),
            FLIPPER_HEIGHT-63 + i*3);

        // slingshots
        makeObject(FLIPPER_CENTER + (s*2-1)*(FLIPPER_SPACE+20+i), FLIPPER_HEIGHT-70-i*3, TYPE_BUMPER, 5);

        // bumper grid
        makeObject(CENTER+(i%3*24)*(s*2-1), BUMPER_CENTER+258-i%9*20, TYPE_BUMPER, 5);
    }
}

Continuing to build the table, here are the walls around the flippers on the bottom and the slingshots. The grid of scoring bumpers in the center is created using a mod operator on the loop variable.

That’s everything to set up the table. It seems like a lot when written out like that but ends up minifying to be very small and then getting a good compression boost from the repetition.

// main game loop
const update = substep=>
{
    // update physics
    for(substep = PHYSICS_SUBSTEPS; substep--;)
    {

Here we have the actual update loop which is called every frame. To improve the physics simulation there are multiple physics steps for each actual update, 9 to be exact. It is implemented as just another loop within the main update loop.

This is necessary to improve the smoothness of the physics and prevent the ball from being able to move through objects when bouncing at high speeds.

        // flippers and shooter
        for(s = FLIPPER_COUNT; s--;)
        {
            // control flipper angle
            objects[s] = Math.max(-1, Math.min(1, 
                objects[s] += objects['zx'[s]]? -.07 : .05));

The flippers and shooter are controlled in this block of code. First we check the input for the z and x keys to control the flipper speed. This is used to update the flipper angles which are stored in objects[0] and objects[1] for the left and right flipper.

            // update flipper and shooter physics
            for(i = FLIPPER_PIECES; i--;)
            {
                // update flippers
                o = objects[1+FLIPPER_COUNT+s*FLIPPER_PIECES+i];
                o.v = -o.x + (o.x = FLIPPER_CENTER + (s*2-1) * 
                    (FLIPPER_SPACE - i*Math.cos(objects[s]/2)));
                o.w = -o.y + (o.y = FLIPPER_HEIGHT + i*Math.sin(objects[s]/2));
                o.r = FLIPPER_RADIUS - i/8;

The physics for the flipper is updated by calculating the new position for each point along the flipper and using that to update the velocity with distance from the previous frame. The velocity will need to be correct for the ball to properly interact with the flipper.

The position of each point along the flipper is stored as it’s own object. A slight taper is added to the flipper radius.

                // update shooter
                o = objects[1+FLIPPER_COUNT+FLIPPER_COUNT*FLIPPER_PIECES+i];
                o.y = Math.min(SHOOTER_MAX_HEIGHT+i,    // clamp shooter pos
                      o.y += o.w = objects['c'] ? .05 : // pull back shooter
                      Math.sin(++frame)/99+             // randomness
                      (SHOOTER_HEIGHT+i-o.y)/19);       // shooter spring
            }
        }

I always thought it was called a launcher but while working on this I found out that the thing you pull back to launch the ball is called the shooter.

This code works similar to the flippers but simpler because there is no rotation. Instead the player presses c to pull back the shooter and it springs up when released.

I found that this was the best place to introduce a tiny bit of randomness. The starting ball path would be deterministic without this extra bit of code to shift the position by Math.sin(++frame)/99. In other words, this ensures that the game starts with a random seed.

        // clear canvas and get ball
        a.width |= o = objects[BALL_INDEX];

        // update ball movement and gravity
        o.x += o.v;
        o.y += o.w += .0017;

        // check if ball is out
        if (o.y > MAX_BALL_HEIGHT && ballCount)
        {
            // respawn ball
            o.x = CENTER+DOME_RADIUS-BALL_RADIUS;
            o.y = FLIPPER_HEIGHT-20;
            o.w = o.v = 0;
            ballCount--;
        }

Here is where we do physics on the ball. Since there is only one moving object we just need to update the ball. This is very basic x and y velocity with gravity applied.

There is a simple test if the ball’s y position is below the screen and there is a ball left then it will respawn the ball in the shooter area.

        // for each object
        objects.map(p=>
        {
            // draw object
            substep || // fix local var being created in minified
                c.beginPath(c.fill(c.arc(p.x, p.y, 
                    p.b ? --p.b + p.r: p.r,0,9)));

Now we need to loop through all the objects to update them and test them for collision with the ball. This is also where we render the objects, drawing the pinball table.

            // get collision distance
            h = Math.hypot(dx = o.x - p.x, dy = o.y - p.y);
            
            // relative velocity
            i = p.v - o.v;
            j = p.w - o.w;

            // resolve collision
            if (h - o.r - p.r < 0 & // is inside
                i*dx + j*dy > 0 &   // moving towards
                !(p.t & !o.v))      // can collide
            {

For each object we need to check if it is colliding with the ball. This is done by checking if the distance from the ball is less then their combined radii.

The objects must be moving towards each other to ensure physics works properly. That same bit of code is also what prevents the ball from colliding with itself.

There is a special check here that allows the ball to pass through the bumper before it is launched by waiting until it has an x velocity to be considered in play.

                // move outside collision
                o.x -= (h - o.r - p.r) * dx / h;
                o.y -= (h - o.r - p.r) * dy / h;

                // tangent length
                h *= h / (j * dx - i * dy);

                // get restitution and update bumper
                s =  !p.t | p.b ?  RESTITUTION :
                (
                    // start bounce animation
                    p.b = 9,

                    // don't give score for slingshots
                    p.y > 600 ? 0 : 
                    
                    // apply score and award extra balls
                    ++score % 64 || ++ballCount,

                    // make it bouncy
                    BUMPER_RESTITUTION
                );

                // reflect velocity and bounce
                o.v += (i + dy / h) * s;
                o.w += (j - dx / h) * s;
            }
        });
    }

Now that we know the ball is colliding we need to resolve the collision. This is done by first moving the ball outside of the collision. Then there is just a little math to get the reflection vector.

If the ball hits a bumper there is extra logic to add to the score and make it bounce more. I put in a check to prevent the bottom slingshots from awarding points to require players to hit the ball up towards the top of the table to score.

    // draw score
    for(i = score+8>>3; i--;)
        drawCircle(CENTER-DOME_RADIUS-40-i%8*20, 420+i*3, i?9:score%8);

    // draw ball count
    for(i = ballCount; i--;)
        drawCircle(CENTER+DOME_RADIUS+60, 420+i*60, 25);
}

To draw the score and balls with very limited space we will reuse the draw circle function. For the score I experimented with many different variations but ended up going with this one for size and readability to the player. This way each row is equivalent to one extra ball, and it also shows progress on the current pip.

// keyboard input
onkeydown = e => objects[e.key] = 1;
onkeyup   = e => objects[e.key] = 0;

setInterval(update, 16); // 60 fps update

All that is left is to get input from the keyboard which is stored in the same array of objects as everything else. In this case they are strings for the keys pressed.

The game runs on a 60 frame per second update loop using set interval.

Minification

My entry starts out at around 6896 bytes for all the code shown above including comments. Then I run an automated process to help minify the code starting with google closure and terser on it to get…

a,b,c,d;let r,t,y,o,h,f,e,i,n,g,x,w=(r,a,t,y=9)=>{n.push({x:r,y:a,t:t,r:y,g:0,w:0})};for(n=[x=3,1],w(i=g=0,1e3),r=65;r--;){for(h=2;h--;)w();w(691,790,0,6)}for(h=2;h--;){for(w(482,816),w(500,180,1,15),w(500+60*(2*h-1),120,1,45),w(500+60*(2*h-1),240,1,45),w(482-210*(2*h-1),320,1,70),r=115;r--;)w(500+209*(2*h-1),800-7*r);for(w(482+182*(2*h-1),539,1,15),r=60;r--;)w(673,800-7*r),w(500+209*(2*h-1)*Math.cos(r/38),209-209*Math.sin(r/38));for(r=19;r--;)w(482+154*(2*h-1),697-7*r),w(482+(2*h-1)*(154-4*r),697+3*r),w(482+(2*h-1)*(100+r),690-3*r,1,5),w(500+r%3*24*(2*h-1),438-r%9*20,1,5)}onkeydown=r=>n[r.key]=1,onkeyup=r=>n[r.key]=0,setInterval((w=>{for(w=9;w--;){for(h=2;h--;)for(n[h]=Math.max(-1,Math.min(1,n[h]+=n["zx"[h]]?-.07:.05)),r=65;r--;)e=n[3+65*h+r],e.g=-e.x+(e.x=482+(2*h-1)*(80-r*Math.cos(n[h]/2))),e.w=-e.y+(e.y=760+r*Math.sin(n[h]/2)),e.r=15-r/8,e=n[133+r],e.y=Math.min(790+r,e.y+=e.w=n.c?.05:Math.sin(++i)/99+(760+r-e.y)/19);a.width|=e=n[2],e.x+=e.g,e.y+=e.w+=.0017,1e3<e.y&&x&&(e.x=691,e.y=740,e.w=e.g=0,x--),n.map((a=>{w||c.beginPath(c.fill(c.arc(a.x,a.y,a.b?--a.b+a.r:a.r,0,9))),f=Math.hypot(y=e.x-a.x,o=e.y-a.y),r=a.g-e.g,t=a.w-e.w,0>f-e.r-a.r&0<r*y+t*o&!(a.t&!e.g)&&(e.x-=(f-e.r-a.r)*y/f,e.y-=(f-e.r-a.r)*o/f,f*=f/(t*y-r*o),h=!a.t|a.b?1.3:(a.b=9,600<a.y||(++g%64||++x),1.7),e.g+=(r+o/f)*h,e.w+=(t-y/f)*h)}))}for(r=g+8>>3;r--;)c.beginPath(c.fill(c.arc(260-r%8*20,420+3*r,r?9:g%8,0,9)));for(r=x;r--;)c.beginPath(c.fill(c.arc(760,420+60*r,25,0,9)))}),16);

This version is pretty small at 1466 bytes but there is more that can be done. We can do some manual edits to remove the variable declarations from the top, simplify the function syntax and wrap the interval code in a quotes.

w=(x,y,t,r=9)=>n.push({x,y,t,r,g:0,w:0});for(n=[x=3,1],w(i=g=0,1e3),r=65;r--;){for(h=2;h--;)w();w(691,790,0,6)}for(h=2;h--;){for(w(482,816),w(500,180,1,15),w(500+60*(2*h-1),120,1,45),w(500+60*(2*h-1),240,1,45),w(482-210*(2*h-1),320,1,70),r=115;r--;)w(500+209*(2*h-1),800-7*r);for(w(482+182*(2*h-1),539,1,15),r=60;r--;)w(673,800-7*r),w(500+209*(2*h-1)*Math.cos(r/38),209-209*Math.sin(r/38));for(r=19;r--;)w(482+154*(2*h-1),697-7*r),w(482+(2*h-1)*(154-4*r),697+3*r),w(482+(2*h-1)*(100+r),690-3*r,1,5),w(500+r%3*24*(2*h-1),438-r%9*20,1,5)}onkeydown=a=>n[a.key]=1,onkeyup=a=>n[a.key]=0,setInterval(`for(w=9;w--;){for(h=2;h--;)for(n[h]=Math.max(-1,Math.min(1,n[h]+=n["zx"[h]]?-.07:.05)),r=65;r--;)e=n[3+65*h+r],e.g=-e.x+(e.x=482+(2*h-1)*(80-r*Math.cos(n[h]/2))),e.w=-e.y+(e.y=760+r*Math.sin(n[h]/2)),e.r=15-r/8,e=n[133+r],e.y=Math.min(790+r,e.y+=e.w=n.c?.05:Math.sin(++i)/99+(760+r-e.y)/19);a.width|=e=n[2],e.x+=e.g,e.y+=e.w+=.0017,1e3<e.y&&x&&(e.x=691,e.y=740,e.w=e.g=0,x--),n.map((a=>{w||c.beginPath(c.fill(c.arc(a.x,a.y,a.b?--a.b+a.r:a.r,0,9))),f=Math.hypot(y=e.x-a.x,o=e.y-a.y),r=a.g-e.g,t=a.w-e.w,0>f-e.r-a.r&0<r*y+t*o&!(a.t&!e.g)&&(e.x-=(f-e.r-a.r)*y/f,e.y-=(f-e.r-a.r)*o/f,f*=f/(t*y-r*o),h=!a.t|a.b?1.3:(a.b=9,600<a.y||(++g%64||++x),1.7),e.g+=(r+o/f)*h,e.w+=(t-y/f)*h)}))}for(r=g+8>>3;r--;)c.beginPath(c.fill(c.arc(260-r%8*20,420+3*r,r?9:g%8,0,9)));for(r=x;r--;)c.beginPath(c.fill(c.arc(760,420+60*r,25,0,9)))`,16)

That shrinks it down to 1416 bytes which isn’t a huge savings but every bit helps. Finally we run it through RegPack to get…

for(_='00F*rE8F-7ED/f)*hCin(BMath.AAsB@keyZ1,Y0,XXYWr=V),UUVT-rS69R15Qe. a.f- r-r-=()**Acos(x,y,t, w x ge=n[--;)for();209+=+rw(482(2*h-1)EU+*(1,X9))60	n[h] y=a=>n[Z]=h=2;h*,;rU5Fc.beginPath(c.fill(c.arc(
w=(V9)=>n.push({r,g:Xw:0}n=[x=3,1],i=g=X1e3T65{);RY79XX6)}{,816,18WQ+	12W45+	24W45U-21032W70T1Q5F+D+182539,YQT	673,D+*r/38U-*@r/38)V19+Q4R7-754-4EUR7+3FUR0-3E,Y5%3*24438S%9*2W5)}onZdownYonZupXsetInterval(`w=9;w{=Amax(-YAmBYn["zx"[h]]?-.07:.05)T653+65*h],=-+(=482+*(80S/2))U=-+(=7	*@/2)U VQS/8,133],=AmB790,=n.c?.05:@++i)/99+(7	-)/19);width|=2],,.F17,1e3<&&x&&(=RY=74X==Xx--Un.map((a=>{w||
x,y,b?--b+r:rUf=Ahypot(y=-x,o=-yTg-,t=w-,0>&0<r*y+t*o&!(t&!)&&(y/f,o/f,f*=f/(t*yS*oUh=!t|b?1.3:(b=9,	0<y||(++g%64||++xU1.7U(r+oC,(t-yC)}))}Vg+8>>3
2	S%8*2X420+3E,r?9:g%8Vx
7	,420+	E,25)`,16)';G=/[
- Q-Z@-F]/.exec(_);)with(_.split(G))_=join(shift());eval(_)

This brings it down to it down to a lean 1013 bytes. That version can unpack itself and then execute that code. This type of compression works by replacing repeated strings with single characters so it looks pretty unreadable in this state. Still a few things jump out like the “c.beginPath(c.fill(c.arc(” that we talked about earlier.

Enhanced Version

I released a slightly enhanced version of the game that includes a few small improvements including…

• mouse and touch support
• improved frame rate smoothness
• responsive canvas size
  • title and byline text

You can play that version directly right here…

See the Pen Lu1ky Pinball 🍀 Tiny pinball physics game in 1K of JS by Frank Force (@KilledByAPixel) on CodePen.

Wrap Up

That should give you a pretty detailed understanding of how my 1k pinball game works, thanks for sticking through to the end. I hope it helps you make your own tiny games, they are a ton of fun! Follow me on twitter for latest updates on all my crazy projects. I will also recommend some of my other 1k projects available on my GitHub…

• Batafuraiko – Retro style shoot-em-up
• 1Keys – Tiny 3 Instrument Piano
• Digilemma – A Digital Dilemma of Devious Difficulty